

This class and its iterator implement all of the As elements are added to a priority queue, its capacity It is always at least as large as the queue The queue retrieval operations poll,Ī priority queue is unbounded, but has an internalĬapacity governing the size of an array used to store theĮlements on the queue. Tied for least value, the head is one of those elements - ties areīroken arbitrarily. The head of this queue is the least element Insertion of non-comparable objects (doing so may result in A priority queue does not permit null elements.Ī priority queue relying on natural ordering also does not permit Provided at queue construction time, depending on which constructor is The elements of the priority queue are ordered according to their 2009.An unbounded priority queue based on a priority heap. Introduction to Algorithms (3rd Edition). All queue applications where priority is involved.Graph algorithms like Dijkstra’s shortest path algorithm, Prim’s Minimum Spanning Tree, etc.
Priority queue time complexity driver#
Driver program to test above functions A utility function to swap two elements Constructor: Builds a heap from a given array a of given size Deletes the highest priority element(key at root). Returns the maximum priority element (key at root) from max heap Void IncreasePriority(int i, int NewPriority)

Increases priority value of node at index i to NewPriority to get index of right child of node at index i to get index of left child of node at index i to get index of parent of node at index i to heapify a subtree with the root at given index Int heap_size // Current number of elements in max heap Int capacity // maximum possible size of max heap Node *harr // pointer to array of elements in heap
Prototype of a utility function to swap two integers A node element having some Value(name) and Priority To regain the property, we shift up the element to its proper position. Otherwise, we need to traverse up to fix the violated heap property. If new item's priority is less than its parent, then we don’t need to do anything. We add a new item with given priority at the end of the tree. Inserting a new element takes O(log 2n) time.
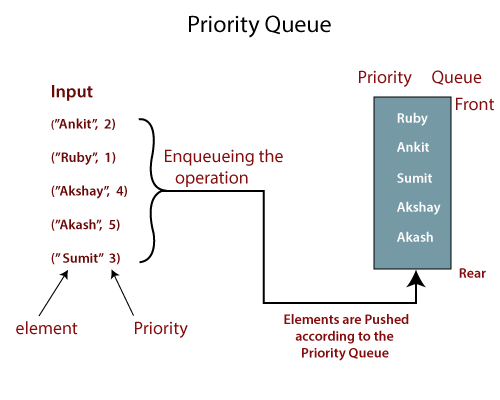
OperationsĪ typical priority queue supports following operations. Doing so, we maintain the Max-Heap property, which is value of any node in the max-heap tree is greater than both of its child. Here we will focus only on implementing max-priority queue using Binary heap (Max-Heap). There are several specialized heap data structures that either supply additional operations or outperform heap-based implementations for specific types of keys, specifically integer keys. It will take O(log 2n) time to insert and delete each element in the priority queue.īased on heap structure, priority queue also has two types max-priority queue and min-priority queue. We can use heaps to implement the priority queue. We can use list and can insert elements in O(n) time and can sort them to maintain a priority queue in O(nlog 2n) time. Suppose we have n elements and we have to insert these elements in the priority queue. Now 2 will be inserted between 4 and 1 as it is smaller than 4 but greater than 1.Īll the steps are represented in the diagram below:Ī simple implementation is to use array of following structure. Now 5 will be inserted between 7 and 4 as 5 is smaller than 7. While inserting 1, as it is the current minimum element in the priority queue, it will remain in the back of priority queue. Now when 7 will be inserted it will moved to front as 7 is greater than 4. Lets say we have an array of 4 elements : and we have to insert all the elements in the max-priority queue.įirst as the priority queue is empty, so 4 will be inserted initially.


 0 kommentar(er)
0 kommentar(er)
